linux內核代碼中廣泛使用了數據結構和算法,其中最常用的兩個是鏈表和紅黑樹。
鏈表
Linux內核代碼大量使用了鏈表這種數據結構。鏈表是在解決數組不能動態擴展這個缺陷而產生的一種數據結構。鏈表所包含的元素可以動態創建并插入和刪除。鏈表的每個元素都是離散存放的,因此不需要占用連續的內存。鏈表通常由若干節點組成,每個節點的結構都是一樣的,由有效數據區和指針區兩部分組成。有效數據區用來存儲有效數據信息,而指針區用來指向鏈表的前繼節點或者后繼節點。因此,鏈表就是利用指針將各個節點串聯起來的一種存儲結構。
(1)單向鏈表
單向鏈表的指針區只包含一個指向下一個節點的指針,因此會形成一個單一方向的鏈表,如下代碼所示。
Struct?list?{ ????int?data;???/*有效數據*/ ????struct?list?*next;?/*指向下一個元素的指針*/ };
如圖所示,單向鏈表具有單向移動性,也就是只能訪問當前的節點的后繼節點,而無法訪問當前節點的前繼節點,因此在實際項目中運用得比較少。
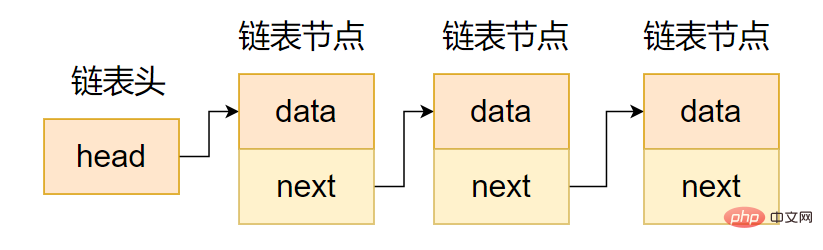
單向鏈表示意圖
(2)雙向鏈表
如圖所示,雙向鏈表和單向鏈表的區別是指針區包含了兩個指針,一個指向前繼節點,另一個指向后繼節點,如下代碼所示。
struct?list?{ ????int?data;???/*有效數據*/ ????struct?list?*next;?/*指向下一個元素的指針*/ ????struct?list?*prev;?/*指向上一個元素的指針*/ };
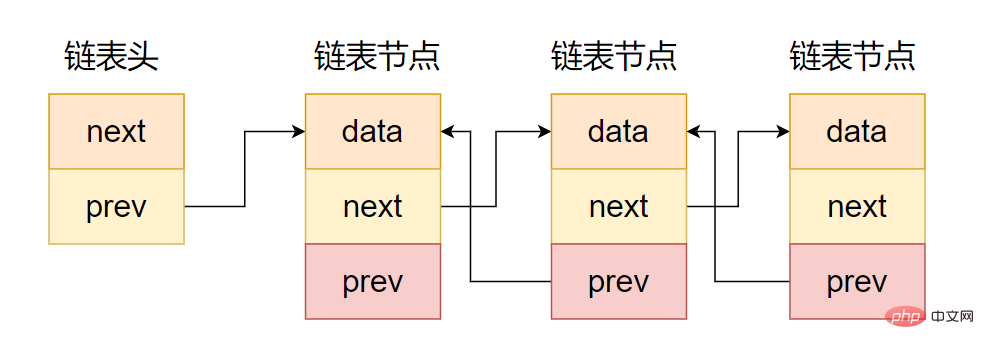
雙向鏈表示意圖
(3)Linux內核鏈表實現
單向鏈表和雙向鏈表在實際使用中有一些局限性,如數據區必須是固定數據,而實際需求是多種多樣的。這種方法無法構建一套通用的鏈表,因為每個不同的數據區需要一套鏈表。為此,Linux內核把所有鏈表操作方法的共同部分提取出來,把不同的部分留給代碼編程者自己去處理。Linux內核實現了一套純鏈表的封裝,鏈表節點數據結構只有指針區而沒有數據區,另外還封裝了各種操作函數,如創建節點函數、插入節點函數、刪除節點函數、遍歷節點函數等。
Linux內核鏈表使用struct list_head數據結構來描述。
<include> struct?list_head?{ ????struct?list_head?*next,?*prev; };</include>
struct list_head數據結構不包含鏈表節點的數據區,通常是嵌入其他數據結構,如struct page數據結構中嵌入了一個lru鏈表節點,通常是把page數據結構掛入LRU鏈表。
<include> struct?page?{ ????... ????struct?list_head?lru; ????... }</include>
鏈表頭的初始化有兩種方法,一種是靜態初始化,另一種動態初始化。
把next和prev指針都初始化并指向自己,這樣便初始化了一個帶頭節點的空鏈表。
<include> /*靜態初始化*/ #define?LIST_HEAD_INIT(name)?{?&(name),?&(name)?} #define?LIST_HEAD(name)? ????struct?list_head?name?=?LIST_HEAD_INIT(name) /*動態初始化*/ static?inline?void?INIT_LIST_HEAD(struct?list_head?*list) { ????list->next?=?list; ????list->prev?=?list; }</include>
添加節點到一個鏈表中,內核提供了幾個接口函數,如list_add()是把一個節點添加到表頭,list_add_tail()是插入表尾。
<include> void?list_add(struct?list_head?*new,?struct?list_head?*head) list_add_tail(struct?list_head?*new,?struct?list_head?*head)</include>
遍歷節點的接口函數。
#define?list_for_each(pos,?head)? for?(pos?=?(head)->next;?pos?!=?(head);?pos?=?pos->next)
這個宏只是遍歷一個一個節點的當前位置,那么如何獲取節點本身的數據結構呢?這里還需要使用list_entry()宏。
#define?list_entry(ptr,?type,?member)? ????container_of(ptr,?type,?member) container_of()宏的定義在kernel.h頭文件中。 #define?container_of(ptr,?type,?member)?({???????????? ????const?typeof(?((type?*)0)->member?)?*__mptr?=?(ptr);???? ????(type?*)(?(char?*)__mptr?-?offsetof(type,member)?);}) #define?offsetof(TYPE,?MEMBER)?((size_t)?&((TYPE?*)0)->MEMBER)
其中offsetof()宏是通過把0地址轉換為type類型的指針,然后去獲取該結構體中member成員的指針,也就是獲取了member在type結構體中的偏移量。最后用指針ptr減去offset,就得到type結構體的真實地址了。
下面是遍歷鏈表的一個例子。
<drivers> static?ssize_t?class_osdblk_list(struct?class?*c, ????????????????struct?class_attribute?*attr, ????????????????char?*data) { ????int?n?=?0; ????struct?list_head?*tmp; ????list_for_each(tmp,?&osdblkdev_list)?{ ????????struct?osdblk_device?*osdev; ????????osdev?=?list_entry(tmp,?struct?osdblk_device,?node); ????????n?+=?sprintf(data+n,?"%d?%d?%llu?%llu?%sn", ????????????osdev->id, ????????????osdev->major, ????????????osdev->obj.partition, ????????????osdev->obj.id, ????????????osdev->osd_path); ????} ????return?n; }</drivers>
紅黑樹
紅黑樹(Red Black Tree)被廣泛應用在內核的內存管理和進程調度中,用于將排序的元素組織到樹中。紅黑樹被廣泛應用在計算機科學的各個領域中,它在速度和實現復雜度之間提供一個很好的平衡。
紅黑樹是具有以下特征的二叉樹。
每個節點或紅或黑。
-
每個葉節點是黑色的。 -
如果結點都是紅色,那么兩個子結點都是黑色。 -
從一個內部結點到葉結點的簡單路徑上,對所有葉節點來說,黑色結點的數目都是相同的。
紅黑樹的一個優點是,所有重要的操作(例如插入、刪除、搜索)都可以在O(log n)時間內完成,n為樹中元素的數目。經典的算法教科書都會講解紅黑樹的實現,這里只是列出一個內核中使用紅黑樹的例子,供讀者在實際的驅動和內核編程中參考。這個例子可以在內核代碼的documentation/Rbtree.txt文件中找到。
#include?<linux> #include?<linux> #include?<linux> #include?<linux> #include?<linux> #include?<linux> #include?<linux> MODULE_AUTHOR("figo.zhang"); MODULE_DESCRIPTION("?"); MODULE_LICENSE("GPL"); ??struct?mytype?{? ?????struct?rb_node?node; ?????int?key;? }; /*紅黑樹根節點*/ ?struct?rb_root?mytree?=?RB_ROOT; /*根據key來查找節點*/ struct?mytype?*my_search(struct?rb_root?*root,?int?new) ??{ ?????struct?rb_node?*node?=?root->rb_node; ?????while?(node)?{ ??????????struct?mytype?*data?=?container_of(node,?struct?mytype,?node); ??????????if?(data->key?>?new) ???????????????node?=?node->rb_left; ??????????else?if?(data->key?rb_right; ??????????else ???????????????return?data; ?????} ?????return?NULL; ??} /*插入一個元素到紅黑樹中*/ ??int?my_insert(struct?rb_root?*root,?struct?mytype?*data) ??{ ?????struct?rb_node?**new?=?&(root->rb_node),?*parent=NULL; ?????/*?尋找可以添加新節點的地方?*/ ?????while?(*new)?{ ??????????struct?mytype?*this?=?container_of(*new,?struct?mytype,?node); ??????????parent?=?*new; ??????????if?(this->key?>?data->key) ???????????????new?=?&((*new)->rb_left); ??????????else?if?(this->key?key)?{ ???????????????new?=?&((*new)->rb_right); ??????????}?else ???????????????return?-1; ?????} ?????/*?添加一個新節點?*/ ?????rb_link_node(&data->node,?parent,?new); ?????rb_insert_color(&data->node,?root); ?????return?0; ??} static?int?__init?my_init(void) { ?????int?i; ?????struct?mytype?*data; ?????struct?rb_node?*node; ?????/*插入元素*/ ?????for?(i?=0;?i?key?=?i; ??????????my_insert(&mytree,?data); ?????} ?????/*遍歷紅黑樹,打印所有節點的key值*/ ??????for?(node?=?rb_first(&mytree);?node;?node?=?rb_next(node))? ??????????printk("key=%dn",?rb_entry(node,?struct?mytype,?node)->key); ?????return?0; } static?void?__exit?my_exit(void) { ?????struct?mytype?*data; ?????struct?rb_node?*node; ?????for?(node?=?rb_first(&mytree);?node;?node?=?rb_next(node))?{ ??????????data?=?rb_entry(node,?struct?mytype,?node); ??????????if?(data)?{ ????????????????rb_erase(&data->node,?&mytree); ????????????????kfree(data); ??????????} ?????} } module_init(my_init); module_exit(my_exit);</linux></linux></linux></linux></linux></linux></linux>
mytree是紅黑樹的根節點,my_insert()實現插入一個元素到紅黑樹中,my_search()根據key來查找節點。內核大量使用紅黑樹,如虛擬地址空間VMA的管理。
無鎖環形緩沖區
生產者和消費者模型是計算機編程中最常見的一種模型。生產者產生數據,而消費者消耗數據,如一個網絡設備,硬件設備接收網絡包,然后應用程序讀取網絡包。環形緩沖區是實現生產者和消費者模型的經典算法。環形緩沖區通常有一個讀指針和一個寫指針。讀指針指向環形緩沖區中可讀的數據,寫指針指向環形緩沖區可寫的數據。通過移動讀指針和寫指針實現緩沖區數據的讀取和寫入。
在Linux內核中,KFIFO是采用無鎖環形緩沖區的實現。FIFO的全稱是“First In First Out”,即先進先出的數據結構,它采用環形緩沖區的方法來實現,并提供一個無邊界的字節流服務。采用環形緩沖區的好處是,當一個數據元素被消耗之后,其余數據元素不需要移動其存儲位置,從而減少復制,提高效率。
(1)創建KFIFO
在使用KFIFO之前需要進行初始化,這里有靜態初始化和動態初始化兩種方式。
<include> int?kfifo_alloc(fifo,?size,?gfp_mask)</include>
該函數創建并分配一個大小為size的KFIFO環形緩沖區。第一個參數fifo是指向該環形緩沖區的struct kfifo數據結構;第二個參數size是指定緩沖區元素的數量;第三個參數gfp_mask表示分配KFIFO元素使用的分配掩碼。
靜態分配可以使用如下的宏。
#define?DEFINE_KFIFO(fifo,?type,?size) #define?INIT_KFIFO(fifo)
(2)入列
把數據寫入KFIFO環形緩沖區可以使用kfifo_in()函數接口。
int?kfifo_in(fifo,?buf,?n)
該函數把buf指針指向的n個數據復制到KFIFO環形緩沖區中。第一個參數fifo指的是KFIFO環形緩沖區;第二個參數buf指向要復制的數據的buffer;第三個數據是要復制數據元素的數量。
(3)出列
從KFIFO環形緩沖區中列出或者摘取數據可以使用kfifo_out()函數接口。
#define????kfifo_out(fifo,?buf,?n)
該函數是從fifo指向的環形緩沖區中復制n個數據元素到buf指向的緩沖區中。如果KFIFO環形緩沖區的數據元素小于n個,那么復制出去的數據元素小于n個。
(4)獲取緩沖區大小
KFIFO提供了幾個接口函數來查詢環形緩沖區的狀態。
#define?kfifo_size(fifo) #define?kfifo_len(fifo) #define?kfifo_is_empty(fifo) #define?kfifo_is_full(fifo)
kfifo_size()用來獲取環形緩沖區的大小,也就是最大可以容納多少個數據元素。kfifo_len()用來獲取當前環形緩沖區中有多少個有效數據元素。kfifo_is_empty()判斷環形緩沖區是否為空。kfifo_is_full()判斷環形緩沖區是否為滿。
(5)與用戶空間數據交互
KFIFO還封裝了兩個函數與用戶空間數據交互。
#define????kfifo_from_user(fifo,?from,?len,?copied) #define????kfifo_to_user(fifo,?to,?len,?copied)
kfifo_from_user()是把from指向的用戶空間的len個數據元素復制到KFIFO中,最后一個參數copied表示成功復制了幾個數據元素。
kfifo_to_user()則相反,把KFIFO的數據元素復制到用戶空間。這兩個宏結合了copy_to_user()、copy_from_user()以及KFIFO的機制,給驅動開發者提供了方便。